异常值发现与处理异常值:
==异常值(Outlier)或利离群点:故意、误差和错误==
异常值的发现
1、人工
最有效,但是最费力
2、简单的统计分析
对于一些错误(不可能)的数据或极小概率时间,如身高出现负数或陨石砸到我头上
有时也会有一些矛盾的、重复的数据,也是异常值
3、3$\delta$原则
在数据服从正态分布的时候,$P(|x-\mu|>3\delta)<=0.003$,对于这种极小概率事件可以视为异常值
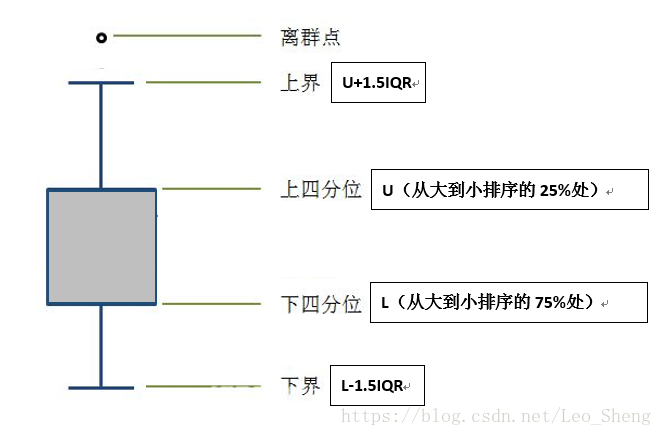
4、箱型图分析(Tukey test)
一些定义
四分
第一四分位数Q1:
- (n+1)/4所表示的数,如果没有整除则带加权。如10.25是的${1\over 4}第10个和{3\over 4}第11个$
中位数Q2:顾名思义
第三四分位数Q3:定义类似第一四分位数
四分位距:IQR=Q3-Q1(这个是数值的距离,Q1234都是数值不是位置)
非异常值范围(内限范围):$[Q1-1.5IQR,Q3+1.5IQR]$ ,这里面的是可接受的,之外的是异常值
外限范围:$[Q1-3IQR,Q3+3IQR]$
- 内外限范围之间的叫做温和异常值
- 外限范围外的叫做极端异常值
如上,变成一个箱子模样的东西
优缺点
- 优点:
- 1、与高斯分布的异常值识别一样简单明了,好实现
- 2、四分位数有一定的抗耐性,就是极端异常数据可以任意远而不影响
- 3、客观
- 缺点:
- 1、假如缺失值大量的集中在一遍,就不能精确衡量
- 举个很简单的例子,有80%的数据是1,19.9%的数据是2,0.1%的数据是10000。这个时候箱型图会把后20%的数据给扔掉。
- 可能你会想,对于这种情况把IQR加上一个较小的数是不是能够解决问题。但是假如10%是2,10%是10000,80%是1,这个时候理论上就没有异常值
- 综上:箱型图适合处理比较散的数据
- 2、数据量大的时候,用四分位数评价有局限性
- 1、假如缺失值大量的集中在一遍,就不能精确衡量
pandas中的实现
1 | data.boxplot() |
5、基于模型检测
上面的两种方法,一个是已经有了模型,另一个是比较散的时候的普遍模型
类似,我们可以自己建立一个概率模型,低概率的对象视为异常点。
优缺点:
- 适用于特征值较少的情况,高维数据检测效果不好
- 有坚实的统计学基础
6、基于聚类
顾名思义,按照聚类的方法,如果一个点不强属于任何一个簇,那么这就是离群点
优缺点:
- 基于线性和接近线性的聚类方法(k-means)对离群点检测是很有效的
- 聚类算法产生的簇的质量对离群点的质量影响很大
- 非常依赖簇的个数(对参数选择敏感)
7、基于邻近度
如knn,如果得到的邻近度比较都比较大,那么就是离群点
优缺点
- 简单
- 慢,大数据不适用
- 对参数选择敏感,如k
- 不能处理有不同密度的数据集(因为选用的是全局阈值k,不能考虑这种密度的不同)
8、基于密度
从密度上来说,离群点就是低密度的地方。
密度通常用邻近度来定义:
- 法1、找k个邻近点,取他们平均值的倒数作为密度
- 法2、范围k中的点的个数
优缺点
- 受到密度区域不同的影响小
- 慢
- 参数选择困难
One Class SVM
不会
Isolation Forest
不会
Robust covariance
好像就是用协方差来搞
异常值处理
1、不处理
一定范围内,减小一定的精确度。
因为对当前数据欠拟合,有时可能也会出现有不可思议的泛化能力
2、删除
对于少量的极端的,如$3\delta$范围外的或箱型图中外限范围外的,删掉会比较好
3、均值替换(单变量)
连续值建议不用众数和中位数来处理,这样容易过拟合。但是离散值可以用众数或中位数
平均值有一定的客观性
4、视作缺失值处理
相当于把异常的东西,试图使其不异常
5、去重
对于一些完全一样,又是在不会重复的情况下
6、盖帽法(单变量)
就是把超出范围的点全部修改为边界值
如:超过$3\delta$的数据全部改为$3\delta$时的值
7、分箱法(主要处理噪声数据)
分箱
- 按深度分箱:每个箱子内的个数一样,按顺序放入
- 按宽度分箱:每个箱中的数据都在一个范围内,这些范围等宽
处理
由于分箱的方法考虑的是相邻的值,所以这是局部平滑的方法。
目的是去噪,将连续数据变成离散数据
平滑方法
按箱的平均值,中位数,众数,边界值……
优缺点
- 优点:增加粒度(数据的细化程度),消除边界的影响
- 缺点:只保留了数据额的宏观特征
8、回归填补法
- 1、先把非异常的数据的模型建立出来
- 2、然后再预测异常值