神经网络
思想来源
神经网络的思想来源于模拟人脑的神经系统的运作,即”神经网络是有具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应”
神经元
总所周知,神经系统的组成单位是神经元。那么要模拟出神经网络,肯定是要有神经元成分的。
M-P神经元模型

这个模型中,一个神经元被其他n个神经元连接,并传递信号$x_i$过来,且每条信息通道上都有权值$w_i$,当前这个神经元也有阈值$b$。
所有的数据在当前这个神经元上通过求和与激活函数$f$整合,输出$y$
$$
y=f(b+\sum_{i=1}^nw_ix_i)
$$
激活函数与阈值的作用类似神经元的兴奋和抑制的关系:当求和大于$-b$时,激活函数则激活;否则不激活
通过许多个这样的神经元连接在一起
典型的激活函数
阶跃函数
$$
f(x)=
\begin{cases}
1& \text{x≥0}\
0& \text{x<0}
\end{cases}
$$
Sigmoid函数
$$
f(x)=\frac{1}{1+e^{-x}}
$$
我们可以发现上面的这个东西其实就是一个线性分类器
单层神经网络(感知机)
简单介绍
感知机中有两个层次:输入层和输出层
- 输入层:处理输入数据和传递,不做任何计算(整个输入层负责一个样本的输入,而不是输入层的每个元素负责一个样本的输入)
- 输出层:负责整合各个输入层来的数据

如上,输入层有三个元素,输出层有两个元素:意味着有三个数据,需要预测两个信息(比如预测一个二维的向量)
因为预测一个和预测两个原理是一样的,所以==下面假设值预测一个信息==
学习策略
感知机是SVM的鼻祖,其思想与SVM前面的一小段部分差不多。
- 首先,假设数据是线性可分的
- 我们试图找到一个超平面$wx+b=0$可以分割两类数据点
- 我们只用分割就行了,不用像SMV那样要求距离和最小
损失函数
假设$y_i\in$ {$0,1$}
对于所有误分类数据来说
$$
y_i(wx_i+b)<0
$$
因此误分类点集合M的所有点到超平面的距离为
$$
\sum_{x_i\in M}-\frac{1}{||w||}y_i(wx_i+b)
$$
我们的目的当然是使这个距离尽量的小
由于几何间隔和代数间隔的关系,上面的问题可以转化成
$$
\sum_{x_i\in M}-y_i(\hat wx_i+\hat b)
$$
(可以理解为把1/||w||当做系数乘了进去)
感知机的原始形式
$$
min_{w,b}L(w,b)=\sum_{x_i\in M}-y_i(\hat wx_i+\hat b)
$$
感知机学习方法是误分类驱动的,所以可以采用梯度下降的方法极小化误分类函数。
因为误分类函数只和被误分类的点有关,所以我们不能采用批量梯度下降,我们针对于某个被误分类的点进行随机梯度下降。
$$
\nabla w=-\sum_{x_i\in M}y_ix_i\
\nabla b=-\sum_{x_i\in M}y_i
$$
所以我们每次随机选取一个被误分类的点进行梯度下降
$$
w <—w+\eta y_ix_i \
b <—b+\eta y_i
$$
$\eta$是学习率(0,1)
收敛性
- 由大量的推导可知,感知机在线性可分的时候是可以收敛的且误分类的次数是有上界的(在指定的时间内能收敛完)。
- 但是在线性不可分的时候是不收敛的,迭代结果会发生震荡(像xor这样的简单的非线性分类任务都无法解决)
而感知机的算法是存在很多解的,所以有时候我们会对超平面增加很多限制,且数据很可能存在线性不可分的情况—->这时候SVM就出场了。
感知机的对偶形式
我们观察一下w和b的梯度下降公式,可以发现w是与xiyi(1<=i<=n)有关的,而b是与y_i(1<=i<=n)有关的。
所以我们设
$$
w=\sum_{i=1}^n \alpha_iy_ix_i\
b=\sum_{i=1}^n \alpha_iy_i
$$
然后我们关于样本i的误分类条件变为
$$
y_i(\sum_{j=1}^n\alpha_jy_jx_j*x_i+b)<=0
$$
其次,我们的参数更新转化为对误分类样本的系数$\alpha$更新
$$
\alpha_i <—-\alpha + \eta\
b <—-b+\eta
$$
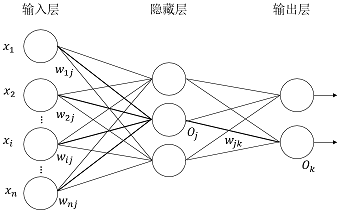
多层前馈神经网络
简单介绍
- 多层前馈神经网络由一个输入层,一个或多个隐藏层和一个输出层
组成
“前馈”:不是指网络中信号不能后传,而是指网络的拓扑结构上不存在环或回路(每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接)
神经网络学习过程,就是分局训练数据来调整神经元之间的“连接权”以及每个功能神经元的阈值,即神经网络学习到的东西,蕴含(隐藏)在连接权和阈值中
误差逆传播算法(BP算法)
- 通常所说的“BP网络”时,一般是指用BP算法训练的多层前馈神经网络

变量定义
有d个输入神经元,l个输出神经元,q个隐层神经元(只有一个隐层)
输出层第j个神经元的阈值$\theta_j$,隐层第h个神经元的阈值$\gamma_h$
第h个神经元的输出为$b_h$
输入层第i个神经元与隐层第h个神经元之间的连接权$v_{ih}$
隐层第h个神经元和输出层第j个神经元之间的连接权$w_{hj}$
隐层第h个神经元接收到的输入为$a_h=\sum_{i=1}^dv_{ih}x_i$
输出层第j个神经元接收到的输入为$\beta_j=\sum_{h=1}^qw_{hj}b_h$
假设所有的激活函数f都是sigmoid函数
对训练样本$(x_k,y_k)$输出:
- $\hat y_k=(\hat y_1^k….y_l^k)$输出是一个l维的向量
- 均方误差$E_k=\frac{1}{2}\sum_{j=1}^l(\hat y_j^k-y_j^k)^2$(前面的0.5是为了后面求导的方便)
学习策略
BP是一个迭代学习算法,在每一轮的迭代中采用广义感知机的规则对参数进行估计(就是对与误差分类有关的参数都梯度下降)
任意参数$v$的更新估计为$v<—v+\Delta v$
如,对于参数$w_{hj}$
$$
\Delta w_{hj}=-\eta \frac{\vartheta E_k}{\vartheta w_{hj}}=\-\eta \frac{\vartheta E_k}{\vartheta \hat y_{j}^k}*
\frac{\vartheta \hat y_{j}^k}{\vartheta \beta_{j}}*
\frac{\vartheta \beta_{j}}{\vartheta w_{hj}}
$$
$$
设g_j=-\frac{\vartheta E_k}{\vartheta \hat y_{j}^k}*
\frac{\vartheta \hat y_{j}^k}{\vartheta \beta_{j}}
$$
因为sigmoid的性质
$$
f’(x)=f(x)(1-f(x))
$$
$$
所以g_j=-\frac{\vartheta E_k}{\vartheta \hat y_{j}^k}*
\frac{\vartheta \hat y_{j}^k}{\vartheta \beta_{j}}\=
-(\hat y_j^k-y_j^k)f’(\beta_j-\theta_j)\=
-(\hat y_j^k-y_j^k)\hat y_j^k(1-\hat y_j^k)
$$
又因为$\frac{\vartheta \beta_{j}}{\vartheta w_{hj}}=b_h$
$$
\Delta w_{hj}=\eta g_jb_h
$$
类似的有
$$
\Delta \theta_j=-\eta g_j\
\Delta v_{ih}=\eta e_hx_i\
\Delta \gamma_h=-\eta e_h\
e_h = b_h(1-b_h)\sum_{j=1}^lw_{hj}g_j
$$
链式规则的缺陷
我们在上面求导的时候,使用了类似函数套函数求导的链式规则。很显然这种做法只是对求导的一个近似。
缺点如下:
- 某个地方梯度过大
- 某个地方梯度过小
一条链的一个部分的梯度与相邻两边差距非常大,这样会影响整体的套数,理论上可以做一些误差调整,这里不做讲述。
特别的:把链式规则的每个地方的元素记录在节点上得到的图叫做计算图
积累BP算法
由于标准的BP算法每次只针对一个数据进行参数的调整,参数更新非常的频繁,有时甚至会出现“抵消”的现象。所以可以考虑对所有数据进行参数调整,梯度为所有数据得到的梯度的平均值。
不过在大数据下,标准的BP算法会表现的比较好。