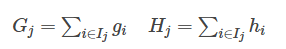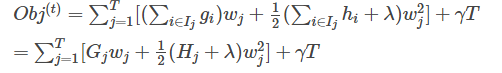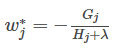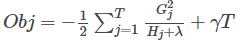0%

XGboost

Posted on Edited on

XGboost

基础GDBT

  • 对于任意函数进行提升树，拟合的残差就是这个函数在当前节点的梯度
  • 最后的多棵树对应的权值加起来

目标函数

定义树的复杂度

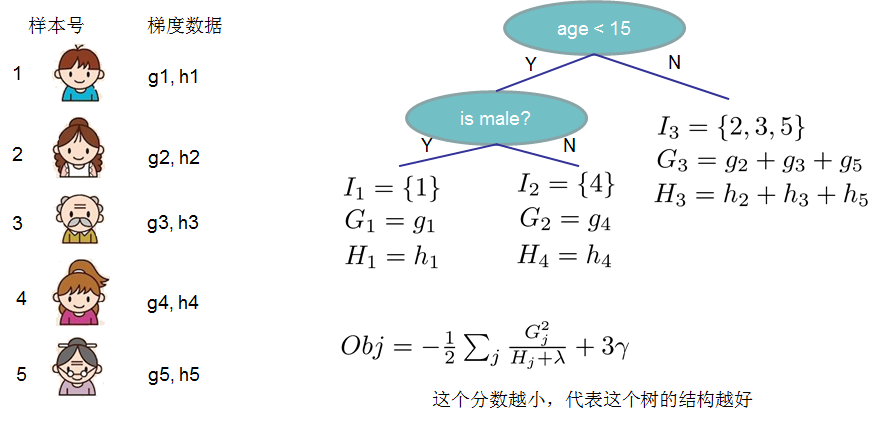
设计XGboost树的结构：树结构和叶子权重

img

定义树的结构的复杂度

img

相当于正则

原始的目标函数

img

假设有t棵树，我们把t棵树的权值加起来就是答案，形式如下

img

我们定义的函数就决定了上面的New function，加上这个==从而使整体距离目标越来越近==。我们把原始目标函数的式子展开就变成下面的东西(constant是一个常数，起到正则作用)img

  • GDBT是使用梯度加上学习率来拟合$f_t$的，XGboost则是多求了一阶的导数(共两阶)，使用泰勒展开

泰勒展开定义目标函数

img

  • 我们假设$f_t(x_i)$就是$\Delta x$，然后对于二元函数$l(y_i,\hat y^{(t-1)})$求关于$\hat y^{(t-1)}$的一阶偏导和二阶偏导，最后用泰勒展开近似$l(y_i,\hat y^{(t-1)}+f_t(x_i))$

  • 再把常数项，和对目标函数优化不影响的$l(y_i,\hat y^{(t-1)})$去掉，剩下的东西就是待优化的如下

img

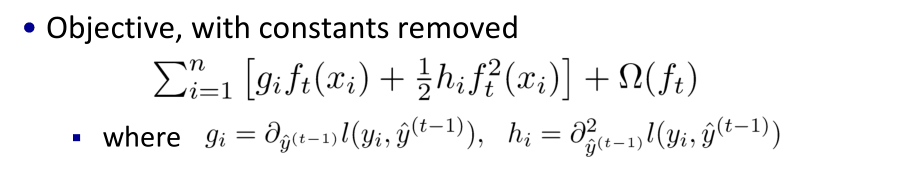
  • 所以与gdbt在函数定义上的区别就是对了个二阶导和正则项

将目标函数变形

  • 首先展开正则项
  • 然后因为$f_t(x_i)$拟合的就是当前节点的分数，所以替换为$w_q(x_i)$
  • 然后考虑将未知参数合并，将$\sum_{i=1}^n\qquad n是样本数$转化成$\sum_{j=1}^T\qquad T是叶子节点数$

img

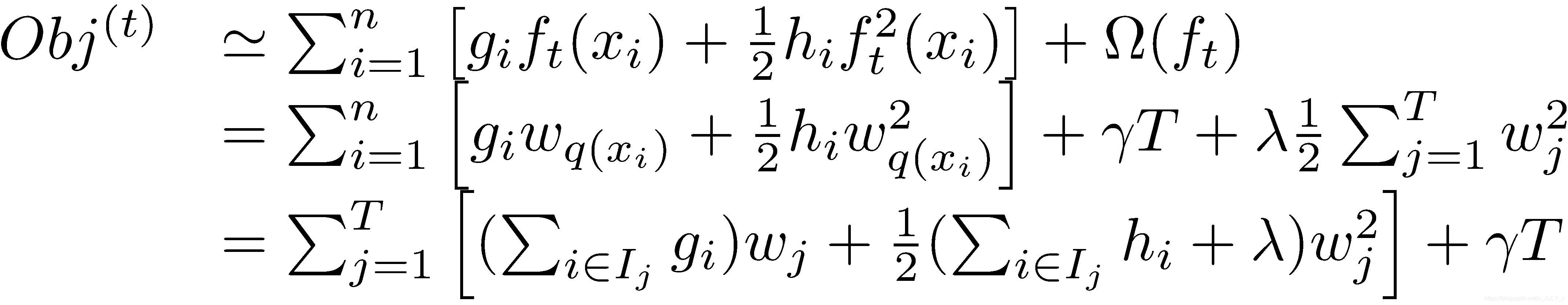
    • 显然$I_x$表示x的叶子x

  • 接着，简化公式

img

img

求导

  • 分别对每个$w_j$偏导

img

img

  • 我们的优化目标就是$Obj$越小越好
  • 例

img

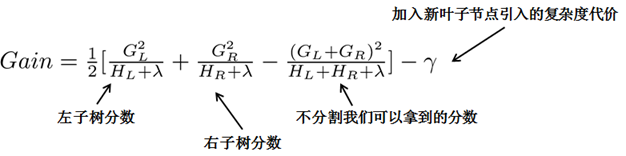
节点的分裂

  • 目标函数千奇百怪，但是对于决策树来说，最关键的还是==最优分割点==

第一种方法：决策树的传统分割(精确贪心算法)

img

不同的就是按照上面目标函数的定义，比平常的分法多了新叶子节点引入的代价，即：不分比分好

img

  • 显然的是时间复杂度还是很高$O(kdn\log n)\qquad k为树的深度，d为特征数$
  • XGboost的单线程版就是这种方法

第二种方法：近似算法

  • 显然的，对于一个特征的分割来说，我们关心的不是这个特征数值的范围，我们寻找的只是特征之间的缝隙，具体点来说——特征百分比
  • 该算法有两种策略(上面的当然也有两种策略)
    • 1、全局近似
      • 在生成一颗树之前就做好了对特征百分比的划分
    • 2、局部近似
      • 在每一层分裂的时候再做对特征百分比的划分

img

带权重的分位数略图（weighted quantile sketch）算法

  • 上面的近似算法每个单位值的权重是1，我们这里改一下，每个单位值的权重是$二阶导h$
  • 我们定义一个数据集Dk = {(x1k, h1), (x2k, h2) … }代表样本的第k个特征及其对应的二阶梯度，现在我们定义一个函数rk：

img

    • 上式表示第k个特征，值z所在数据的比例
  • 且候选集的目标要使得相邻的两个候选分裂点相差不超过阈值(这个阈值当然也是百分数)$\epsilon$，就是规定最小间距
  • 下图为不同的百分数比较与两种策略比较

在这里插入图片描述

为什么用二阶导作为权重

在这里插入图片描述

  • 对于平方误差：权重恒为2，所以相当于不带权
  • 对于log loss：h=p(1-p)，是开口朝下的二次函数。当p在0.5附近，值较大，也就是权重都比较大，在切直方图时，我们希望每个柱子都比较均匀，因此这部分就会被切分的更细。
  • 总的来说就是基于二阶导的含义：梯度的梯度，梯度若波动大，预测则不稳定，样本权重高，切分的更细

稀疏自适应分割

  • 产生数据稀疏的原因主要有三个：
    • 1、数据缺失
    • 2、统计上的0
    • 3、one-hot编码
  • 以往的经验表明，当出现稀疏、缺失值时，算法需要很好的自适应，就是适应稀疏数据。
  • XGboost提出：在计算分割后的分数时，遇到缺失值，分别将缺失值带入左右两个分割节点，然后取最大值的方向为其默认方向（就是把缺失的东西全部当做-∞或+∞）

img

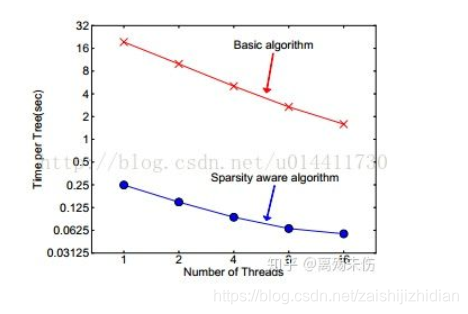
当出现稀疏情况的时候，稀疏性计算只有线性的计算复杂度。如图所示，稀疏自适应算法比基本的非稀疏数据算法快大约50倍。

img

其他优化

采用随机森林的列抽样和行抽样

  • 行采样：用自助法(BootStrapping)。也就是在采用的样本集合可能会出现重复
  • 列采样：从M个feature中，选择m个，然后对于这些特征来搞

这样即能降低过拟合风险，又能降低计算。

库的使用

加载数据

1
2
3
4
可以加载多种数据：
	libsvm格式的文本数据
	numpy的二维数组
	XGBoost的二进制缓存文件。加载的数据储存在对象DMatrix中
1
2
3
4
5
6
7
8
libsvm格式
	dtrain = xgb.Matrix('xxx.svm.txt')
二进制缓存
	dtrain = xgb.DMatrix('xxx.svm.buffer')
加载numpy的数组
	data = np.random.rand(5, 10)    #5行10列数据集
	label = np.random.randint(2, size=5)
	dtrain = xgb.DMatrix(data, label=label)

xgb.sklearn.XGBClassifier(sklearn接口)

​ 优点：使用简单，无需对标签进行标准化处理，直接得到预测标签；

​ 缺点：在模型保存后重新载入，丢失LabelEncoder，不能增量训练只能用一次.

参数设置(参数非常多，下面是一部分)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
clf = XGBClassifier(
silent=0 ,#是否开启静默模式，0为不开启，1为开启，开启后不输出任何信息，显然这不利于我们调参，默认选0就好了
nthread=4,# cpu 线程数 默认最大
learning_rate= 0.3, # 学习率
min_child_weight=1, 
# 这个weight是二阶导，就是用"带权重的分位数略图"算法中的权重。定这个值可以避免分割不均衡
max_depth=6, # 最大树的深度
gamma=0,  # 树的叶子节点上作进一步分区所需的最小损失减少,越大越保守，一般0.1、0.2这样子。
subsample=1, # 下采样比例
max_delta_step=0,#最大增量步长，我们允许每个树的权重估计。
colsample_bytree=1, # 生成树时进行的列采样 
reg_lambda=1,  # L2正则化项参数
reg_alpha=0, # L1 正则项参数
scale_pos_weight=1, #如果取值大于0的话，在类别样本不平衡的情况下有助于快速收敛。平衡正负权重
objective= 'multi:softmax', #多分类的问题 指定学习任务和相应的学习目标,还有binary:logistic和multi:softprob
num_class=10, # 类别数，多分类与 multisoftmax 并用
n_estimators=100, #迭代次数，也是树的个数
seed=1000 #随机种子
eval_metric= 'auc'，#怎么计算目标函数值，根据你目标函数的形式来，对于回归问题，默认值是rmse，对于分类问题，默认值是error。
tree_method# 有三个可选的值， {‘auto’, ‘exact’, ‘approx’} 分别对应上面的三个算法
)

对于eval_metricimg

xgb.train(xgb原生接口)

xgboost原生接口，数据需要经过标签标准化(LabelEncoder().fit_transform)、输入数据标准化(xgboost.DMatrix)和输出结果反标签标准化(LabelEncoder().inverse_transform)，训练调用train预测调用predict.

需要注意的是，xgboost原生接口输出的预测标签概率矩阵各行的下标即为标准化后的label标签(0~class number-1).

1
2
3
xgboost.train(params,dtrain,num_boost_round=10,evals(),obj=None,
feval=None,maximize=False,early_stopping_rounds=None,evals_result=None,
verbose_eval=True,learning_rates=None,xgb_model=None)
  • parms: 这是一个字典，包含着训练中的参数关键字和对应的值，形式是parms={‘boosts’:’gbtree’,’eta’:0.01}
  • dtrain: 训练的数据
  • num_boost_round: 迭代的次数
  • evals: 只是一个列表，用于训练过程中进行评估列表中的元素evals = [(dtrain,’train’),(dval,’val’)] 或者是 evals =[(dtrain,’train’)] ，第一种情况可以在训练的时候观察验证集的效果
  • obj：自定义目标函数
  • early_stopping_rounds：早起停止次数，假设为100，验证集的误差迭代到一定程度在100次内不能再继续降低，就停止迭代
  • evals_result：字典，存储在watchlist中的元素的评估结果
  • verbose_eval（可以输入布尔型或者数值型）：也要求evals里至少有一个元素，如果为True，则对evals中元素的评估结果会输出在结果中；如果输入数字，假设为5，则每隔5个迭代输出一次。
  • learning_rates：每一次提升的学习率的列表
  • xgb_model：在训练之前用于加载的xgb_model

训练

直接用上面那个东西就能训练了bst = xgb.train( plst, dtrain, num_round, evallist )

预测

1
2
dtest = DMatrix(X_test)
ans = model.predict(dtest)

保存模型

1
2
3
4
5
6
bst.save_model('test.model')

# 导出模型到文件
bst.dump_model('dump.raw.txt')
# 导出模型和特征映射
bst.dump_model('dump.raw.txt','featmap.txt')

加载模型

1
2
bst = xgb.Booster({'nthread':4}) # init model
bst.load_model("model.bin")   # load data