0%

对抗自编码器(AAE).md

Posted on

对抗自编码器(AAE)

  • 自编码器转换成生成模型

  • 通过两个目标训练：传统的重构误差函数和对抗训练函数—>将AE隐藏层向量表示的聚合后验分布与任意先验分布匹配。训练准则和VAE很像

    • 1、编码器学到将数据分布转换成该先验分布
    • 2、解码器学到一个模型，可以将强加的先验映射到数据分布上

聚合后验分布

  • 与VAE不同的是，AAE采用的是聚合后验分布

$$
q(z)=\int_{x}q(z|x)p_d(x)dx\
(q(z|x)：编码分布;p(x|z):解码分布；p_d(x)数据分布;\
p(x)数据模型分布;q(z):z的聚合后验分布;p(z):想要在z上加的先验分布)
$$

  • img
  • img
    • AAE是，通过将聚合后验$q(z)$和任意先验$p(z)$进行匹配来完成正则化，让对抗网络直到$q(z)$去匹配$p(z)$
    • 在“指导”的同时，AE也尝试着最小化重构误差
    • 对抗网络的生成器(同时也是AE的编码器)要确保聚合的后验分布可以愚弄对抗网络的判别器，让其误认为隐藏编码$q(z)$来自真实的先验分布$p(z)$
  • 对抗网络好和AE通过SGD基于两个阶段联合训练：基于mini-batch执行重构阶段和生成阶段
    • 1、重构阶段：AE更新编码器和解码器，并最小化重构误差
    • 2、正则阶段：对抗网络首先更新判别网络，以区分真实样本(先验生成的)和生成样本(通过AE计算的隐藏编码)；然后对抗网络再更新生成器(AE的编码器)

对于$q(z|x)$的分布

是个确定函数

  • 不多说

高斯后验

  • 类似VAE的，用混合高斯加网络预测

通用近似后验Universal approximator posterior

假设AAE的编码网络是函数$f(x,\eta)$，输入x和固定分布(如高斯)的随机噪声。

通过在$\eta$的不同样本上评估$f(x,\eta)$，从而从任意的后验分布$q(z|x)$中进行采样

  • 假设$q(z|x,\eta)=\delta(z-f(x,\eta))$

  • 那么后验$q(z|x)$和聚合后验$q(z)$定义如下

    • $$
      q(z|x)=\int_{\eta}q(z|x,\eta)p_{\eta}(\eta)d\eta \Rightarrow \q(z)=\int_{x}\int_{\eta}q(z|x,\eta)p_d(x)p_{\eta}(\eta)d\eta dx
      $$
  • 此时，$q(z)$的随机性同时来自数据分布和编码器输入上的随机噪声$ \eta$
    • 在上面是确定函数的情况下，因为$q(z|x)$是确定的，网络正让$q(z)$取匹配$p(z)$，只利用了数据分布的随机性。然而数据的经验性分布是被训练集固定的，映射是确定的，这可能生成一个不是很平滑的$q(z)$
    • 然而，高斯或通用近似的情况中，网络需要额外的随机性来源，来帮助在对抗正则阶段对$q(z)$进行平滑惩罚

说了这么多，作者在多次试验后发现，上面三种方法的结果大同小异。。。。。。

  • 所以后面只介绍$q(z|x)$的确定性策略

与VAE的关系

VAE：使用的是KL散度惩罚的方法在隐藏层编码向量上强加一个先验分布(如高斯分布)

AAE：使用的是对抗训练方法去实现该目的，即让隐藏层编码向量的聚合后验能够匹配先验分布

VAE：最小化关于-log的似然上边界

img

  • 这里的变分边界有三个部分：第一个重构项，第二第三个相当于正则项，没有正则项就是简单的AE，有正则项的时候，VAE学到的隐藏层表征与$p(z)$是兼容的。

    • 损失函数的第二项鼓励后验分布
    • 第三项是最小化后验$p(z)$与先验$q(z)$的交叉熵

  • 而AAE中：作者将后面的两项替换成了一个对抗学习的过程，从而鼓励$q(z)$能与$p(z)$整个分布匹配

对插入特定先验的能力做对比

img

  • 上图是在MNIST上训练的
    • A、B是AAE的，分别是单个2维高斯和10个混合的二维高斯
    • C、D是VAE的，与上面类似
  • 1、如A可以看到，AAE在学习流形(不同类别的转化)有明显的转变(分界线)，且没有空洞；所以VAE对于抓去数据流行的能力并没有AAE好
  • 2、VAE与AAE得到的分布类似，不过VAE表现出与10个组件高斯混合的强烈差别，即VAE更多强调匹配的分布模式，AAE则能成功抓取带有先验分布的聚合后
  • 3、一个重要的差别是：VAE中，为了通过MC采样对KL散度进行BP，需要得到准确的先验分布的函数形式；而在AAE中，只需要能从先验分布中进行采样就能让$q(z)$匹配$p(z)$

对抗正则中插入标签信息

  • GAN模型的一个问题就是无法很好的利用数据标签信息，这里，AAE对此提供了一个很不错的解决办法

这里的数据都是标记过的，可以将标签信息插入到对抗训练过程中，a来更好的塑造隐藏层的分布

  • 不过在该结构中，我们要使用部分或者所有的标签信息来更好的正则化Ae的潜在表征

img

  • 上图是一个半监督的训练过程，这里增加了一个one-hot向量到判别网络的输入部分，以将标签与分布模式相结合，这个one-hot有一定的决策作用
    • one-hot向量除了带有每个标签的维度，还有一个额外维(无标签的样本类别，如生成器的样本)
      • 如上面的mnist，one-hot有11个类别
  • 当一个无标签样本出现在该模型中，额外的类别就会相应，以选择整个高斯混合分布的决策面
    • 1、在对抗训练的正阶段(最大化识别)：通过one-hot将高斯混合模型生成的样本的标签传给判别器。这些正样本来自混合高斯模型，而不是来自某个具体的类别(第一个高斯产生的样本是1,第二个是2,…)
    • 2、在对抗训练的负阶段：通过one-hot将生成器生成的样本的标签给判别器。这些负样本来自生成器

img

  • (d是沿着swiss roll 来生成的)
    • a：显示了使用先验训练的对抗性自编码的潜在表示，先验训练在10k个有标签mnist和40k个无标签mnist样本，在10个混合的高斯模型上训练。先验中第i个混合惩罚以半监督的方式和第i个类别有关。
    • b：前三个混合成分的流形每个混合成分的类型,表征是很一致的，且与各自的类相独立(例如所有的左上区域对应于直立书写样式，右下区域对应于数字的倾斜书写样式)
    • c(将数据扩展到任意分布而不用参数控制):如将数据映射到一个swiss roll(如条件高斯分布,其均值是均匀分布,长度相当于一个swiss roll 轴),这种方法可以
    • d:是沿着swiss roll轴前进生成的图像

监督

  • 所以监督的方法就是：网络结构为decoder提供一个由标签编码的one-hot，然后decoder利用one-hot识别标签，利用z(以高斯混合的形式)来重构数据。这里的one-hot是对应类别的维度sendpix0

半监督

  • 半监督的方法就是：上面的方法的one-hot对应类别的维度+1

sendpix1

  • 我们我们假设数据是由隐藏的类别变量(分类分布生成)y和高斯分布生成的z共同生成的
  • 我们用encoder: $q(z,y|x)$预测离散和连续的隐变量，然后decoder利用类别标签作为一个热向量和隐变量来重建数据。然后有两个独立的对抗网络规范自编码器的隐藏表示
    • 第一个对抗网络对标签施加分类分布，对抗性网络确保了潜在的类变量不携带任何样式信息，并且让y的聚合后验分布与类别分布相匹配
    • 第二个对抗网络对z施加高斯分布，以确保潜在变量为连续高斯分布变量

无监督聚类

  • 流程与半监督类似，不过去掉了分类阶段

  • 另一个不同的是，$q(y|x)$预测的是一个一维的one-hot，其维数是我们希望将数据聚类得到的类别数sendpix2

  • 上图表示在mnist有16个簇的时候的情况，每行中第一个表示簇头，通过样式变量固定为0并通过标签变量设置为16中的一个数字来生成。其余的图像是随机变量

实现

  • 对于mnist，首先就是编码

encoder

  • 这是decoder，得到最后的输出就是隐藏变量z的维度(在VAE中有两中这样的东西分别是均值和方差，最后用来给z采样)，不过这里并没有假设z是高斯分布，而是聚合后验，就直接用网络拟合(…到后来越来越网络)

然后就是

decoder

假如z还是假设是高斯采样的

img

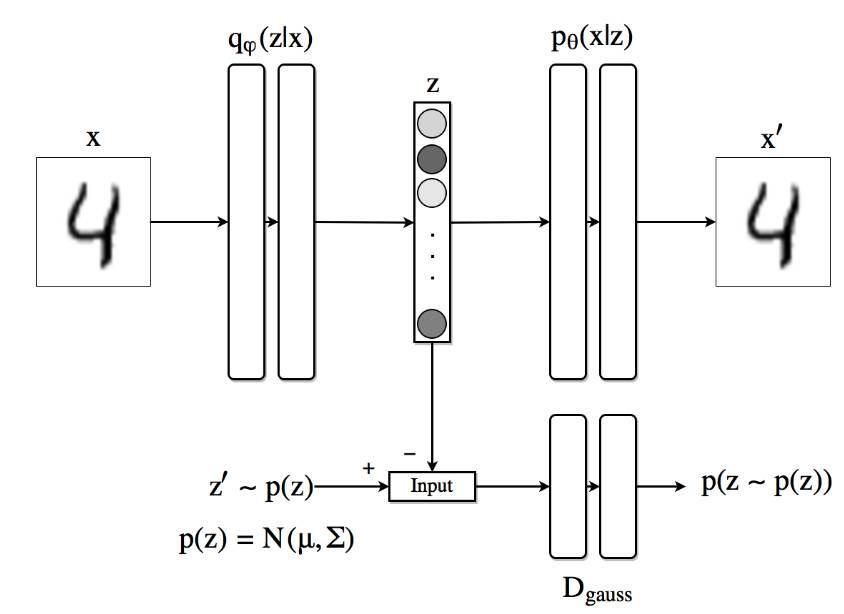
  • 生成的z对对抗网络做负作用，采样的z做正作用
  • img

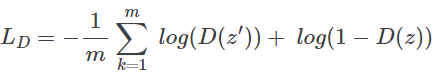
这就是经典的GAN公式了开发者自述：我是这样学习 GAN 的

  • 监督

  • img

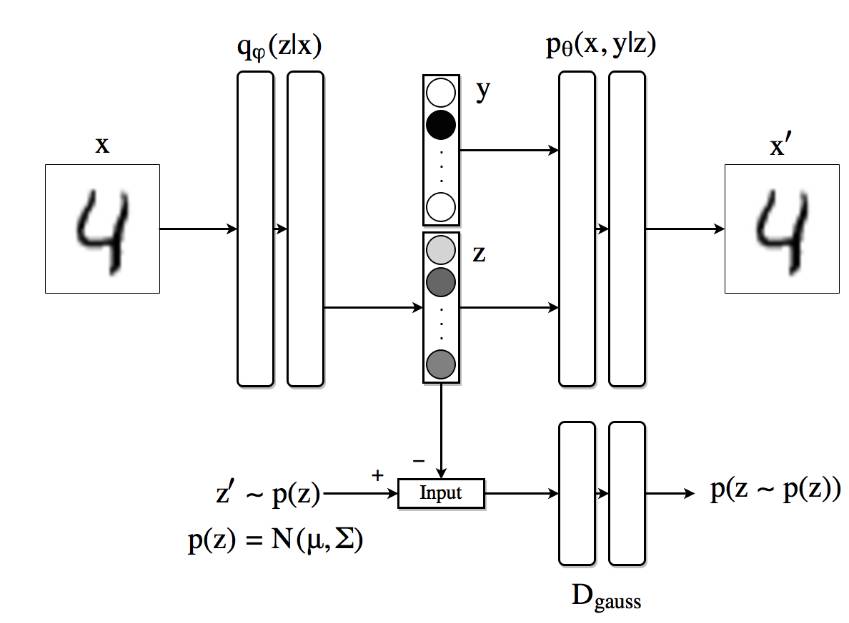
  • 这里把y和z拼起来即可

  • 半监督

  • img

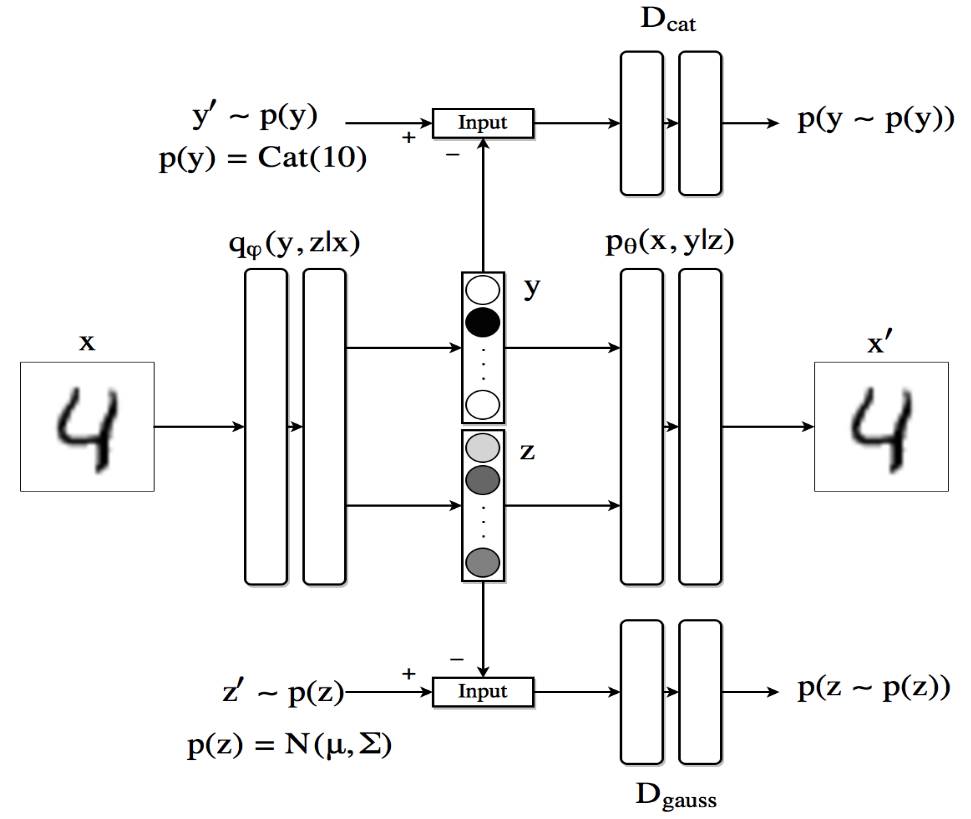
  • 上面的y是一个softmax，然后cat(10)是一个one-hot，就是用GAN拟合one-hot

    • 对于无标签的，就在encoder出生成z和y，然后拟合分布
    • 对于有标签的，就调整生成y时的分布(即encoder的y_fake，就是只到生成y_fake这一步，然后用交叉熵loss)
  • 无监督
    • 就是没有上面的分类，然后one-hot的维数是聚类预估的簇数